|
Hugh M Blackburn |
Semtex is a 'classical' quadrilateral spectral element incompressible direct numerical simulation code that uses the standard nodal GLL basis functions to provide two-dimensional solutions and (optionally) Fourier expansions in a homogeneous direction to provide three-dimensional solutions. If your fluid mechanics problem is two-dimensional or has a natural periodic coordinate direction in 3D (a cylindrical coordinate system is perhaps the most obvious example), semtex could be a good choice. For 3D problems of this kind, the code can run in parallel using MPI to distribute jobs over a number of processes; semtex is equally at home on Unix machines from laptop to supercomputer.
The code's lineage can be traced back through Ron Henderson's prism code and ultimately to the original spectral element code nekton. One noteworthy distinction from other distributions is that semtex supports cylindrical as well as Cartesian coordinates, and with full spectral convergence in all directions. The user is able to include a range of distributed body forces, such as Euler and Coriolis forces, and to include advection of a scalar. In addition to an incompressible Navier–Stokes solver, source is also provided for an elliptic solver that will deal with Laplace, Poisson and Helmholtz problems, as well as for a linear stability analysis and optimal transient growth solver, and a solver for flows with generalized Newtonian rheologies.
Semtex has been compiled and run on a variety of Unix systems. As a minimum, you will need C++, C and F77 (or later FORTRAN) compilers, the Gnu version of make, also cmake, yacc (or bison), as well as BLAS and LAPACK libraries and their associated header files. For parallel compilation and execution you'll need MPI libraries and headers. Most of these things are readily available on modern Unix systems.
The current semtex release can be accessed as a git repository from https://gitlab.com/semtex-base/semtex. Use the 'master' branch or specific tagged releases. Consult the top-level README.md file for installation instructions. Latex source for the user guide is available in the doc folder, but here is a compiled PDF (though perhaps slightly dated) version.
Please note that semtex is a research code and is provided 'as-is' with the understanding that it will be used mainly by other computer-literate researchers in computational fluid dynamics. It is not guaranteed to work or to provide correct results, and neither I or any employer accept any liability for detriment or loss consequent on your use of the code. Please see the terms of the Gnu General Public License (GPL) under which the code is released for public use. On the other hand, I'd be happy to hear of your experiences with using the code and your types of applications and results.
If through your use of the code you manage to obtain publishable results, I would be pleased if you could cite Blackburn, Lee, Albrecht and Singh (2019), where the numerical methods and use of semtex are described. If you also used the linear stability/optimal transient growth solver dog, the appropriate reference is Barkley, Blackburn & Sherwin (2008). For solutions computed using the generalized Newtonian solver gnewt, please cite Blackburn, Rudman & Singh (2025).
I'm afraid that I do not have much time to answer routine questions about making semtex compile, running examples, etc. Please consult the user guide for information on these matters. I will be happy to hear of bugs, and even better, suggestions about how to fix them, although I cannot promise to remedy problems on a timely basis. The source code distribution is occasionally updated, however, the code is quite mature now and the basics do not often change.
Designed to provide a stand-alone introduction sufficient to allow a student to progress to the subsequent course on aircraft design.
This course ranges from conceptual design and initial baseline design through to baseline configuration development. Since by its nature design is an iterative process, the ordering of some topics below might appear somewhat arbitrary — in the early stages of design, one may have to cherry-pick some information from later topics and then return in more depth at a later stage.
A classic experiment by Ludwig Prandtl (circa 1930) provided convincing support for the circulation theory of lift generated by airfoils. Accelerating an airfoil from rest in an initially stationary fluid, circulation is generated in such a way that the net amount is zero; this leaves a starting vortex in the fluid and a net circulation of opposite sign bound to the airfoil. If the airfoil is then bought to rest, the bound circulation is shed from the airfoil in the form of a stopping vortex, leaving the overall circulation in the fluid zero, as it was in the beginning. This animation (Wang & Blackburn 2018) illustrates the process using a two-dimensional simulation of flow generated by a NACA-0012 airfoil at 4o angle of attack and a peak translational Reynolds number of 10,000. Vorticity in the starting vortex is coloured red, while that in the stopping vortex is coloured blue. Note the additional detail of a smaller pair of vortices generated during the stopping process near the leading edge on the airfoil's upper surface.
This animation of axial vorticity for azimuthal Fourier modes 1, 5 and 6 helps to illustrate a triadic resonance instability mechanism for flow in a precessing, rotating cylinder of fluid (Albrecht, Blackburn, Lopez, Manasseh & Meunier 2015). The animations are seen in the frame of reference of the cylinder, in which the forcing directly driven by precessional acceleration occurs in Fourier mode 1 and rotates with the precession frequency. Theory dictates that the other two modes which directly participate in the triad must differ by 1 in azimuth (6-5=1) and counter-rotate in the cylinder frame, exactly as seen here.
Animation of bypass transition in pulsatile stenotic pipe flow in which the pulse waveform represents typical flow in the human common carotid artery (Mao, Sherwin & Blackburn 2010). Linear transient energy growth is extremely large, of order 1×1025 within half a pulse period for suitable initial disturbances at Reynolds number Re=300. For even a tiny seeding with the optimal initial disturbance, a puff of turbulence is generated downstream of the stenosis. This washes slowly downstream and decays during subsequent pulse cycles. Mean flow is from left to right and the stenosis is to the left of the field of view.
Animation of transient two-dimensional convective instability in flow over a backward-facing step at Re=500 (Blackburn, Barkley & Sherwin 2008, Barkley, Blackburn & Sherwin 2008), visualised as contours of perturbation vorticity. The optimal disturbance initial condition is a wave packet that is very tightly clustered around the step edge, and grows into an array of counter-rotating rollers that fill the downstream channel, at a location past both (upper and lower) separation zones, before eventually decaying. The maximum two-dimensional energy growth at this Reynolds number is 63.1×103.
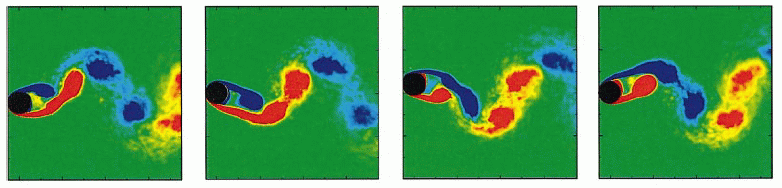
The flow generated by a circular cylinder moving from side to side in quiescent fluid has a number of different instability modes, depending on the amplitude and period of the motion. This image of massless particles advected by a quasi-periodic instability mode shows how small puffs form up into large-scale vortices that move away from the cylinder along the axis of oscillation (Elston, Blackburn & Sheridan, 2006).
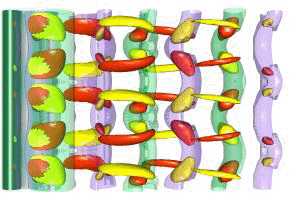
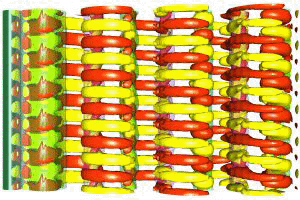
| Mode A, Re=195 | Mode B, Re=265 | Mode TW, Re=400 |
 |
 |
 |
| t=t0 | t=t0+T/2 |
 |
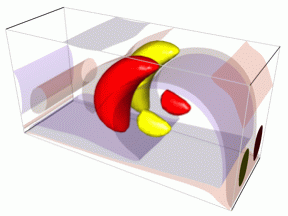 |
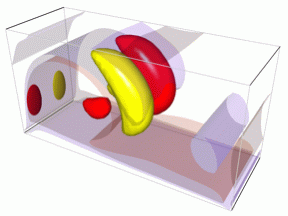
| Periodic axisymmetric state, Re=3000 | Rotating wave with 6-fold symmetry, Re=4000 |
|
|
|
Instabilities of the flow produced by steady rotation of the lower lid of a cylindrical cavity with height/radius ratio H/R=2.5. At low Reynolds numbers the flow is axisymmetric, steady, and has an axial vortex breakdown. The flow first becomes unstable to a periodic axisymmetric instability through a Hopf bifurcation at Re=2707, but at higher Reynolds numbers rotating waves also become unstable, and are modulated by the axisymmetric pulsation. Blackburn & Lopez (2000), Blackburn (2002), Blackburn & Lopez (2002).
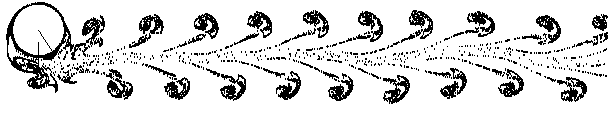
| raw |  |
| filtered |  |